Lindström quantifier

In mathematical logic, a Lindström quantifier is a generalized polyadic quantifier. They are a generalization of first-order quantifiers, such as the existential quantifier, the universal quantifier, and the counting quantifiers.They were introduced by Per Lindström in 1966.

Generalization of first-order quantifiers

In order to facilitate discussion, some notational conventions need explaining. The expression

\phi^{A,x,\bar{a}}=\{x\in A\colon A\models\phi[x,\bar{a}]\}

for A an L-structure (or L-model) in a language L,φ an L-formula, and 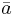\bar{a} a tuple of elements of the domain dom(A) of A. In other words, 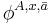\phi^{A,x,\bar{a}} denotes a (monadic) property defined on dom(A). In general, where x is replaced by an n-tuple 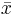\bar{x} of free variables, 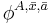\phi^{A,\bar{x},\bar{a}} denotes an n-ary relation defined on dom(A). Each quantifier 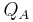Q_A is relativized to a structure, since each quantifier is viewed as a family of relations (between relations) on that structure. For a concrete example, take the universal and existential quantifiers ∀ and ∃, respectively. Their truth conditions can be specified as

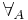A\models\forall x\phi[x,\bar{a}] \iff \phi^{A,x,\bar{a}}\in\forall_A
A\models\exists x\phi[x,\bar{a}] \iff \phi^{A,x,\bar{a}}\in\exists_A,

where \forall_A is the singleton whose sole member is dom(A), and 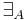\exists_A is the set of all non-empty subsets of dom(A) (i.e. the power set of dom(A) minus the empty set). In other words, each quantifier is a family of properties on dom(A), so each is called a monadic quantifier. Any quantifier defined as an n>0-ary relation between properties on dom(A) is called monadic. Lindström introduced polyadic ones that are n>0-ary relations between relations on domains of structures.

Before we go on to Lindström's generalization, notice that any family of properties on dom(A) can be regarded as a monadic generalized quantifier. For example, the quantifier "there are exactly n things such that..." is a family of subsets of the domain a structure, each of which has a cardinality of size n. Then, "there are exactly 2 things such that φ" is true in A iff the set of things that are such that φ is a member of the set of all subsets of dom(A) of size 2.

A Lindström quantifier is a polyadic generalized quantifier, so instead being a relation between subsets of the domain, it is a relation between relations defined on the domain. For example, the quantifier 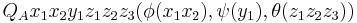Q_Ax_1x_2y_1z_1z_2z_3(\phi(x_1x_2),\psi(y_1),\theta(z_1z_2z_3)) is defined semantically as

A\models Q_Ax_1x_2y_1z_1z_2z_3(\phi,\psi,\theta)[a] \iff (\phi^{A,x_1x_2,\bar{a}},\psi^{A,y_1,\bar{a}},\theta^{A,z_1z_2z_3,\bar{a}})\in Q_A

where

\phi^{A,\bar{x},\bar{a}}=\{(x_1,\dots,x_n)\in A^n\colon A\models\phi[\bar{x},\bar{a}]\}

for an n-tuple 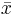\bar{x} of variables.

References